After I started implementing the schedule generator about a week ago, mainly because I wanted to program something again, I realized that it’s not as easy as I thought: Even the scheme that Justin and I worked out when he reviewed my thesis may generate invalid schedules.
The central realization we had back then, and which probably has been clear to most everyone anyway, including me a while ago before I forgot again, was that we need to consider permutations of critical blocks, but the blocks within a thread do not move; they always stay in the same order. If a thread executes the code {A1; A2}, then this is never going to turn into {A2; A1}. Therefore, what we’re actually permuting are opportunities for threads to execute the next block, whichever that may be.
As an example, if we have two threads A and B that fall apart into the critical blocks {A1; A2} and {B1; B2; B3}, respectively, we have to execute the following ten schedules:
A1; A2; B1; B2; B3 A1; B1; A2; B2; B3 A1; B1; B2; A2; B3 A1; B1; B2; B3; A2 B1; A1; A2; B2; B3 B1; A1; B2; A2; B3 B1; A1; B2; B3; A2 B1; B2; A1; A2; B3 B1; B2; A1; B3; A2 B1; B2; B3; A1; A2
The number 10 makes sense since we’re first choosing all the possible combinations of two out of the total of five blocks assigned to thread A, and then all the possible combinations of three blocks out of the remainder of three blocks assigned to thread B (not really a “choice” anymore, since B just gets the leftovers):
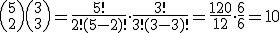
I was almost done with support code to write a scheduler that creates these kinds of lists when I realized that I can’t really come up with a Java program in which all of these schedules were valid. In most Java programs, or at least in the idealized ones I’m considering now, program execution starts with just the main thread; the main thread may then spawn other threads. We could therefore have the threads A and B with the blocks {A1 fork B; A2} and {B1; B2; B3}, respectively, where fork B marks the point thread B is started, or inversely, the point before which thread B did not execute. The point at which thread B is started is not an critical block itself but rather the critical point that delineates the blocks A1 and A2.
If we now examine the list of schedules above and consider the inverse meaning of the fork point, we realize that the following six schedules are invalid since they schedule parts of thread B before it has been started:
B1; A1 fork B; A2; B2; B3 B1; A1 fork B; B2; A2; B3 B1; A1 fork B; B2; B3; A2 B1; B2; A1 fork B; A2; B3 B1; B2; A1 fork B; B3; A2 B1; B2; B3; A1 fork B; A2
To obtain the valid set of schedules, we can consider {A1 fork B} a prefix of all schedules which we do not have to permute, and only deal with the remaining four blocks (for clarity, I showed the prefix only in the first schedule):
A1 fork B; A2; B1; B2; B3
B1; A2; B2; B3
B1; B2; A2; B3
B1; B2; B3; A2
Now we just have four schedules left, as predicted by the product of s-combinations:  .
.
Ok, good. What if one thread waits for another thread to die, i.e. there’s a join point as with the blocks {A1 fork B; A2} and {B1; B2 join A; B3} for threads A and B, where join A marks the point at which thread A waits for thread B to die, or more interestingly, the point after which thread A does not execute anymore. Therefore, the following schedules are all invalid, because part of A executes after the join point:
A1 fork B; B1; B2 join A; A2; B3
B1; B2 join A; B3; A2
We have to consider {A1 fork B} a prefix and {B2 join A; B3} a suffix of all schedules and only permute for the remaining two slots, yielding only two valid schedules: 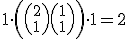 .
.
A1 fork B; A2; B1; B2 join A; B3
B1; A2;
Looks like a relatively simple task now; once a prefix or suffix have been determined, we recursively process the middle part. There are a few problems, though:
- I need to know which thread gets forked and joined. Unique thread IDs give me that information.
- Java may have
join()calls with timeouts, interruptions frominterrupt()calls, and even spurious wake-ups. - Java programs do not have to conform to a fork-join model.
I’ll have to think about how much the lack of a fork-join model impacts schedule generation. Forks definitely exist, so I can avoid scheduling a thread before it is running, but what should I do about the end of threads? If there is no join point, then they can be scheduled at any time, of course, but if there is a join point, then they probably should not be scheduled after it, although Java makes a join() almost meaningless. Maybe the default should be treating a join() as real join point, and optionally making it… meaningless.
I also have to consider whether I can create a connection between wait() and notify()/notifyAll() calls similar to the fork-join model, although that would not only require unique thread IDs, but also unique object IDs.


